Homology of Level Sets
The following images are generated by a haskell library I am writing for applied topology. The first step is to generate the level sets using the marching cubes algorithm, which I've implemented in haskell. Then next part is to compute the persistent homology via left or sub level set filtration; this also includes ideas from large scale geometry.
1 Barnes et al.
Julie Barnes, William Kreahling, and Beth Schaubroeck published a Coloring Book of Complex Function Representations. This coloring book has several pretty images generated via level sets of complex valued functions. Since the book is available for purchase, I thought the images in the book needed barcodes; hence my interest in the project.
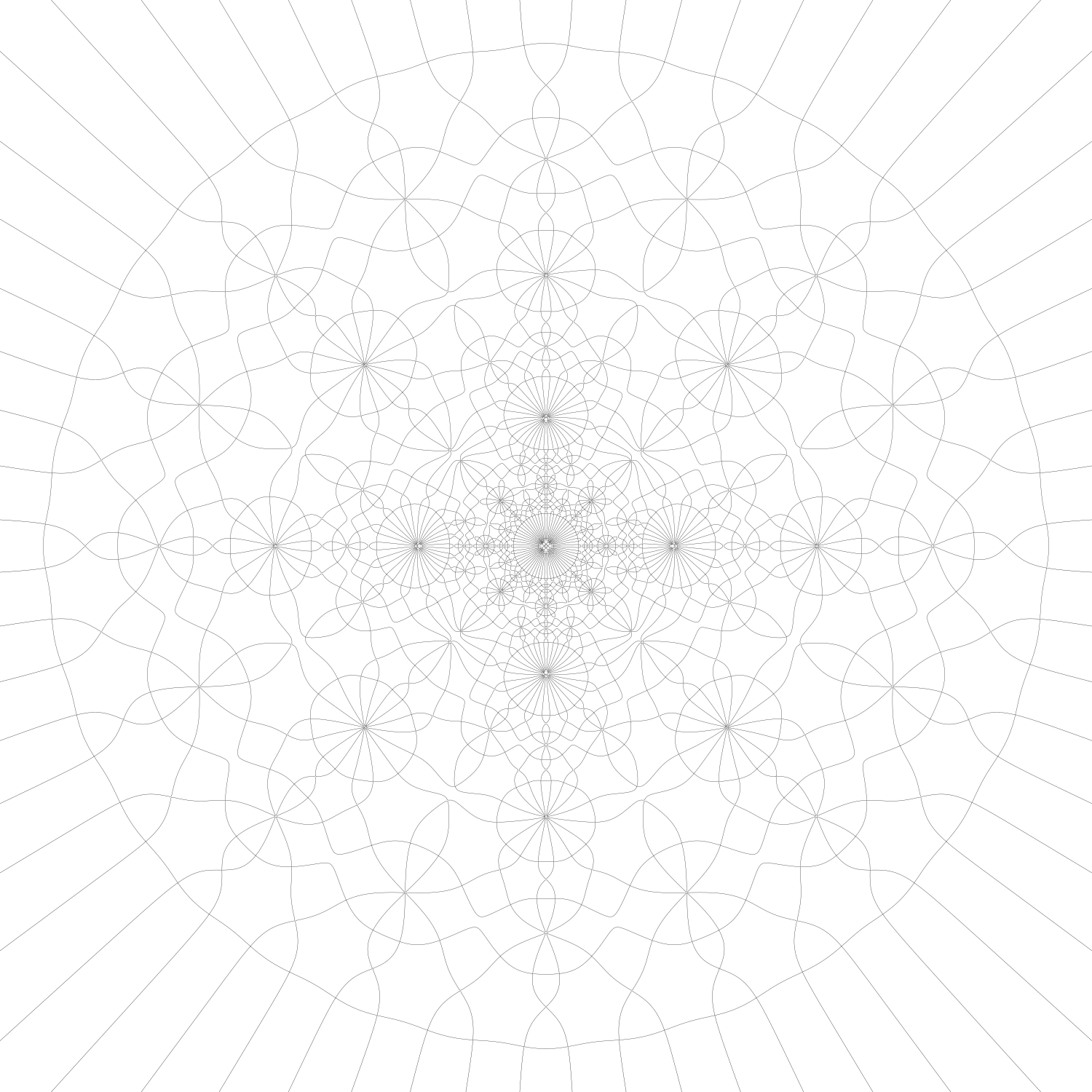
And here is a pdf of the image with its barcode generated by left level set filtration.
2 Batman Logo
This image looks strikingly similar to the Batman Logo.
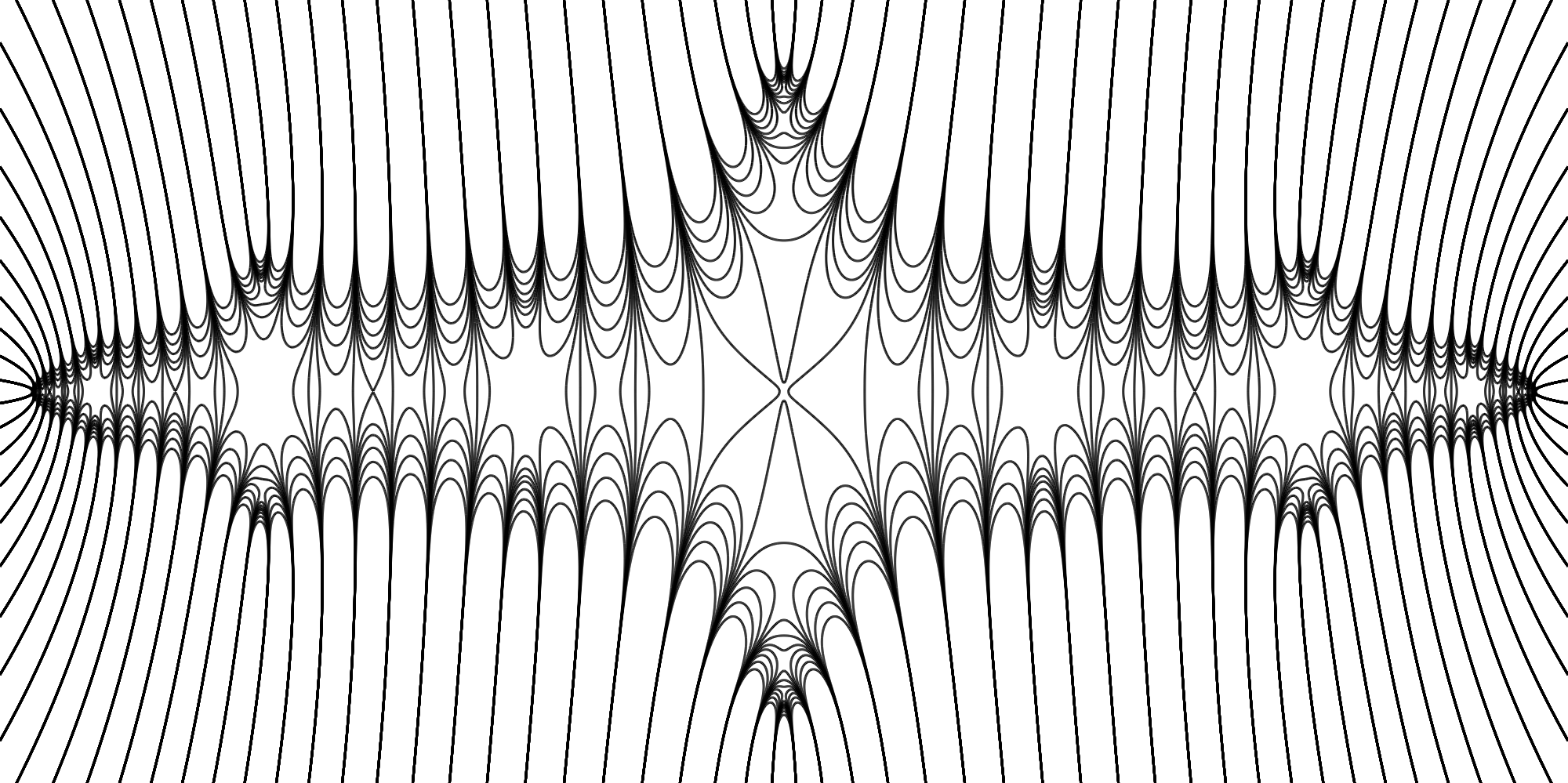
And here is a pdf of the image with its barcode generated by left level set filtration.